Publications
(For a more detailed list of publications of AI Chair OceaniX go to Google Scholar, ResearchGate)
Group highlights
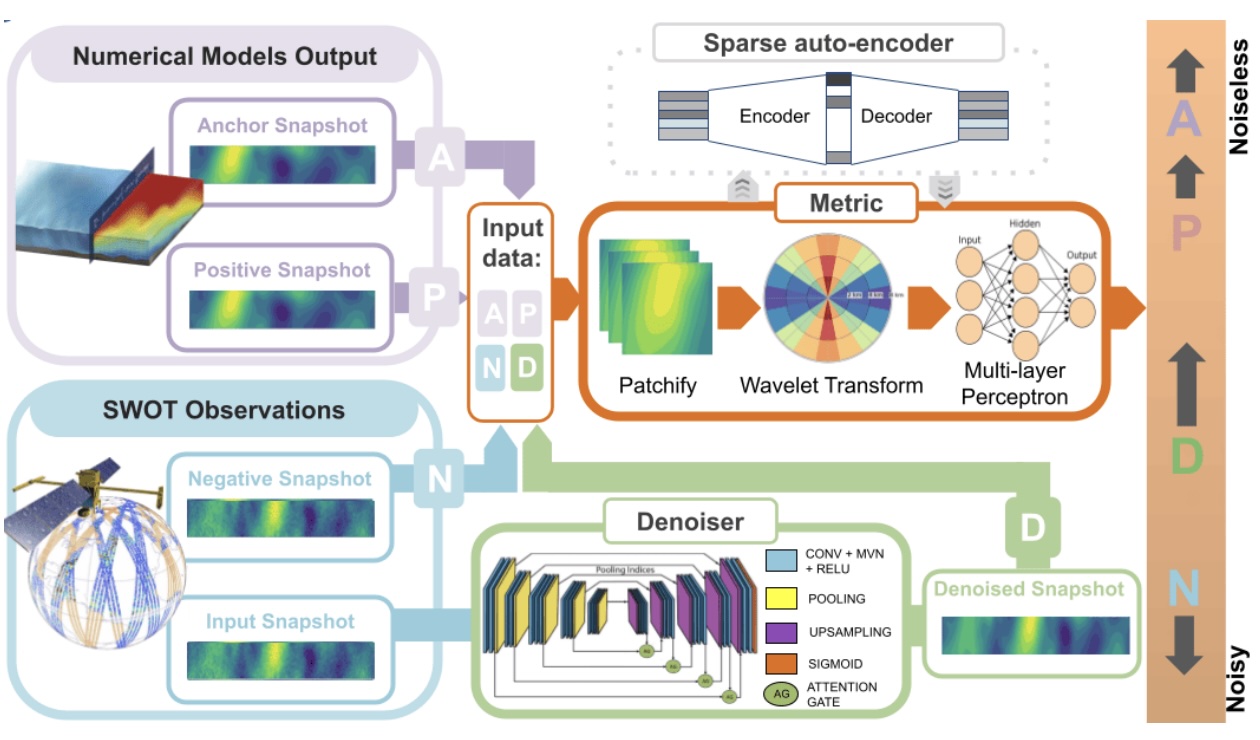
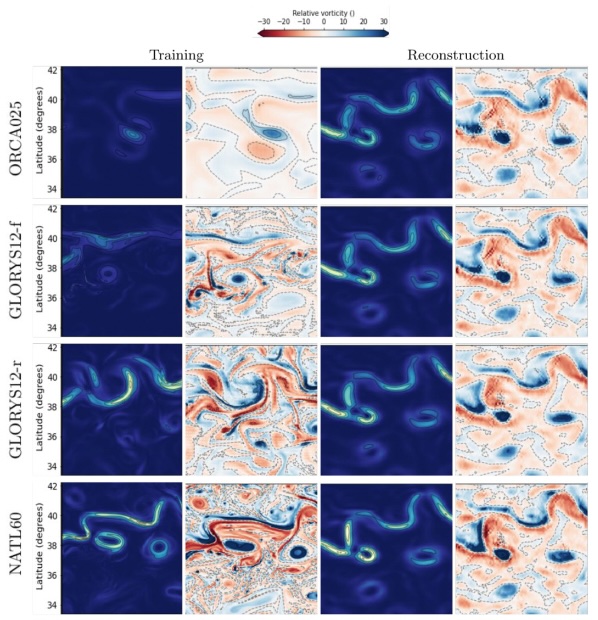
We introduce SIMPGEN, Simulation-Informed Metric and Prior for Generative Ensemble Networks, an unsupervised adversarial learning framework combining real SWOT observations with simulated reference data. SIMPGEN leverages wavelet-informed neural metrics to distinguish noisy from clean fields, guiding realistic SSH reconstructions. Applied to SWOT data, SIMPGEN effectively removes noise, preserving fine-scale features better than existing neural methods. This robust, unsupervised approach not only improves SWOT SSH data interpretation but also demonstrates strong potential for broader oceanographic applications, including data assimilation and super-resolution.
E. Cutolo, C. Granero-Belinchon, P. Thiraux, J. Wang, R. Fablet.
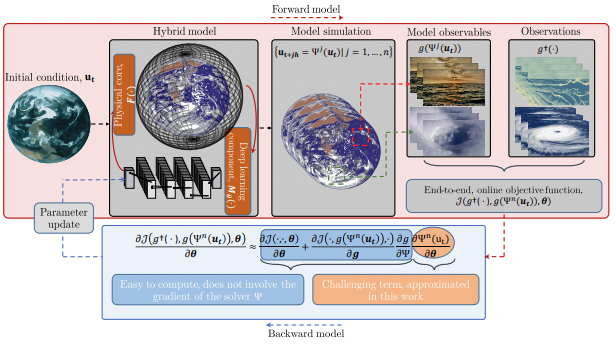
Online learning methodologies thus require the numerical model to be differentiable, which is not the case for most modeling systems. To overcome this difficulty and bypass the differentiability challenge of physical models, we present an efficient and practical online learning approach for hybrid systems. The method, called EGA for Euler Gradient Approximation, assumes an additive neural correction to the physical model, and an explicit Euler approximation of the gradients. We demonstrate that the EGA converges to the exact gradients in the limit of infinitely small time steps. Numerical experiments are performed on various case studies, including prototypical ocean-atmosphere dynamics.
S. Ouala, B. Chapron, F. Collard, L. Gaultier, R. Fablet.
In this study, we conducted a series of numerical Lagrangian experiments in the Porcupine Abyssal Plain region of the North Atlantic and developed a machine learning approach to predict the surface origin of particles trapped in a deep-ocean sediment trap. Our numerical experiments support the predictive performance of the machine learning approach, and surface conditions appear to provide valuable information for accurately predicting the source area, suggesting a potential application with satellite data. We also identify factors that potentially affect prediction efficiency, and we show that the best predictions are associated with low kinetic energy and the presence of mesoscale eddies above the trap.
Febvre et al.
We simulate Lagrangian drift on the sea surface and investigate deep learning approaches to address the shortcomings of current model-based and Markovian approaches, particularly concerning error propagation and computational complexity. We present a novel deep learning framework, referred to as DriftNet, inspired by the Eulerian Fokker-Planck representation of Lagrangian dynamics. Through numerical experiments for simulated and real drift trajectories on the sea surface, we illustrate the effectiveness of DriftNet compared to existing state-of-the-art schemes. We also delve into the influence of diverse geophysical fields, whether derived from models or observations, used as inputs by DriftNet on drift simulation.
Marcille et al.
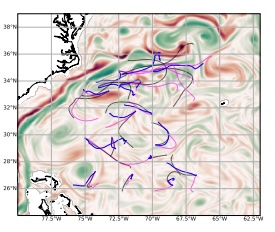
We simulate Lagrangian drift on the sea surface and investigate deep learning approaches to address the shortcomings of current model-based and Markovian approaches, particularly concerning error propagation and computational complexity. We present a novel deep learning framework, referred to as DriftNet, inspired by the Eulerian Fokker-Planck representation of Lagrangian dynamics. Through numerical experiments for simulated and real drift trajectories on the sea surface, we illustrate the effectiveness of DriftNet compared to existing state-of-the-art schemes. We also delve into the influence of diverse geophysical fields, whether derived from models or observations, used as inputs by DriftNet on drift simulation.
Botvinko et al.
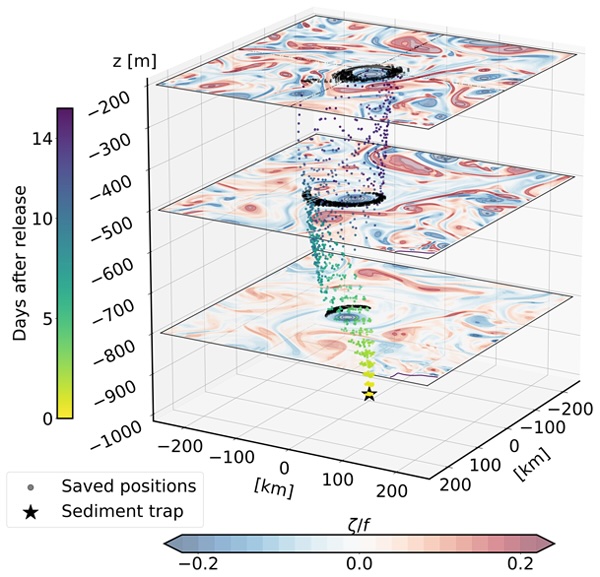
In this study, we conducted a series of numerical Lagrangian experiments in the Porcupine Abyssal Plain region of the North Atlantic and developed a machine learning approach to predict the surface origin of particles trapped in a deep-ocean sediment trap. Our numerical experiments support the predictive performance of the machine learning approach, and surface conditions appear to provide valuable information for accurately predicting the source area, suggesting a potential application with satellite data. We also identify factors that potentially affect prediction efficiency, and we show that the best predictions are associated with low kinetic energy and the presence of mesoscale eddies above the trap.
Febvre et al.
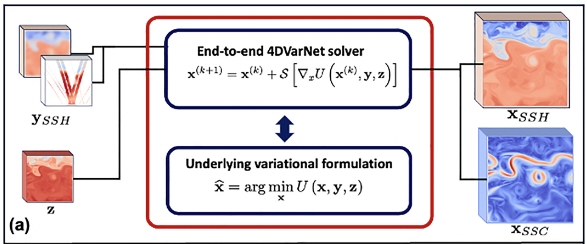
Satellite altimetry provides a unique means for direct observation of sea surface currents, but it is confined to the geostrophic component, limiting the recovery of a substantial portion of mesoscale sea surface currents in operational products. To address this limitation, we present a novel deep learning framework, rooted in a variational data assimilation paradigm, that unlocks new avenues for leveraging the synergistic relationships between satellite-derived sea surface observations, namely sea surface height and sea surface temperature. This innovative scheme demonstrates its remarkable potential to enhance sea surface current reconstruction and recover a substantial portion of the elusive ageostrophic dynamics.
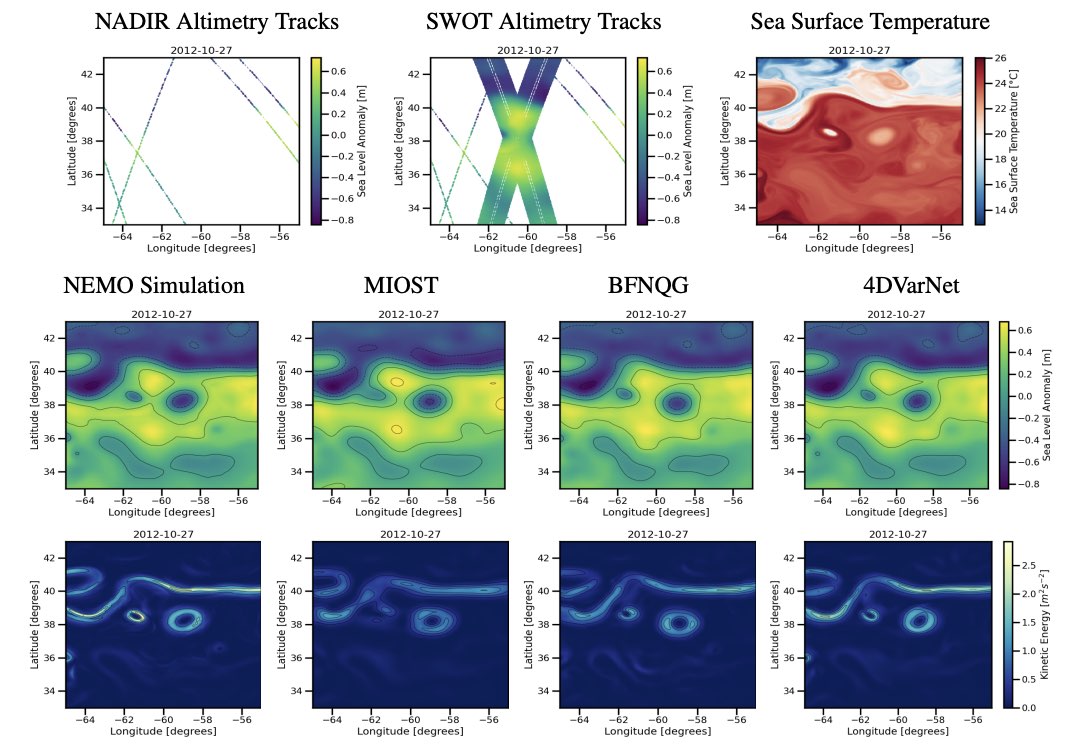
OceanBench is a unifying framework that provides standardized processing steps that comply with domain expert standards for the development and evaluation of deep learning schemes for physical oceanography. It is designed with a flexible and pedagogical abstraction. it provides plug-and-play data and pre-configured pipelines for ML researchers to benchmark their models w.r.t. ML and domain-related baselines and delivers a transparent and configurable framework for researchers to customize and extend the pipeline for their tasks.
J.E. Johnson, Q. Febvre, A. Gorbunova, S. Metref, M. Ballarotta, J. Le Sommer, R. Fablet.
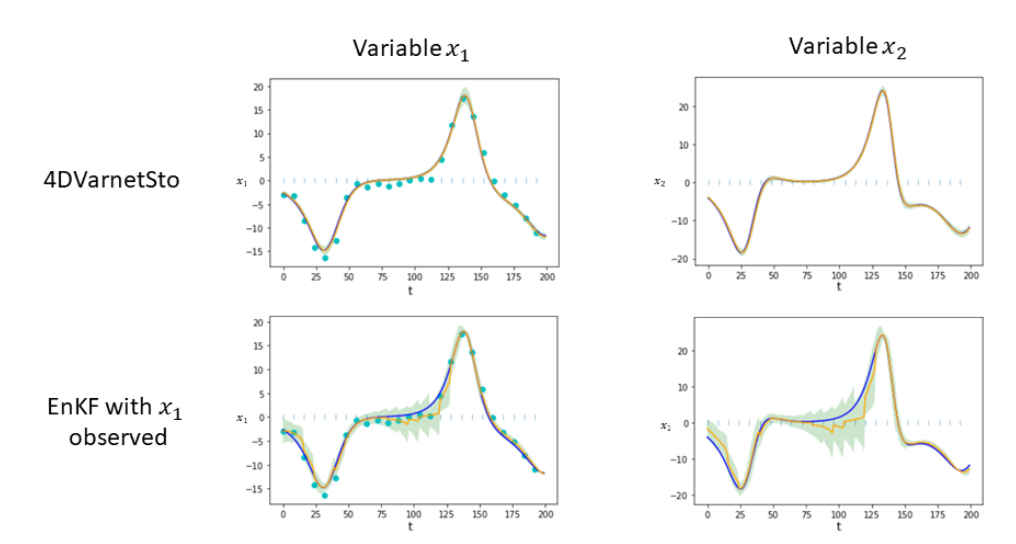
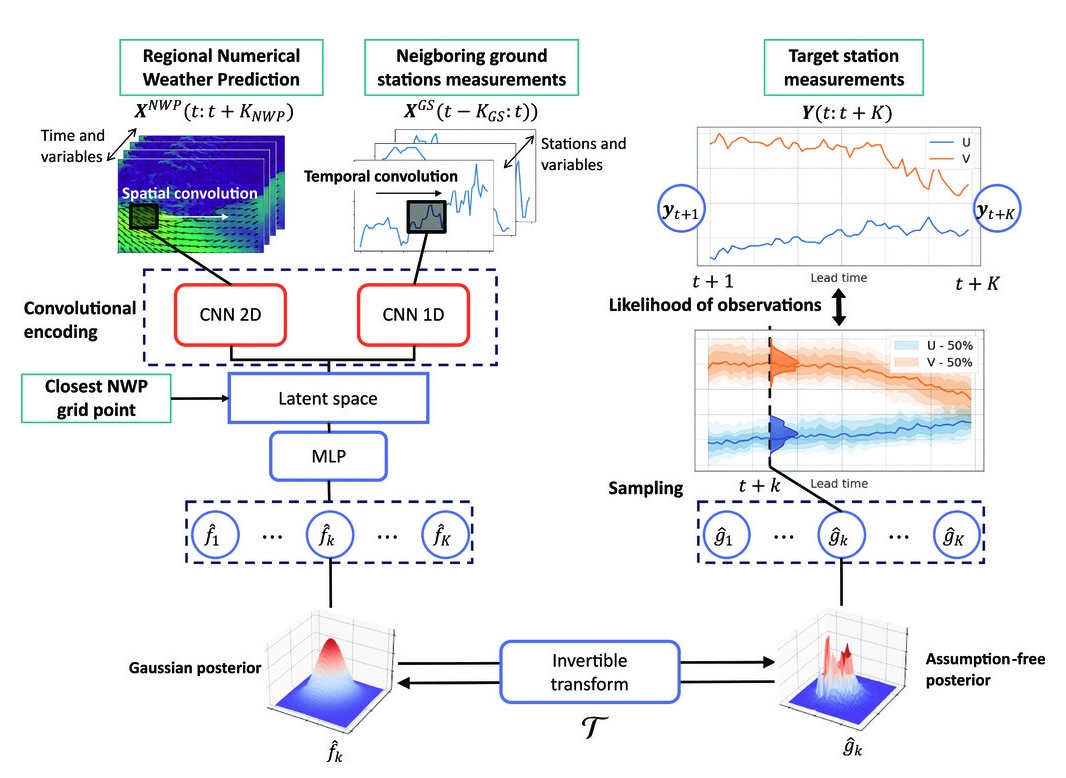
This study proposes an end-to-end Neural Network (NN) scheme based on a Variational Bayes (VB) inference formulation. It combines an ELBO (Evidence Lower BOund) variational cost to a trainable gradient-based solver to infer the state posterior pdf given observation data. The inference of the posterior and the trainable solver are learnt jointly. We demonstrate the relevance of the proposed scheme for a Gaussian parameterization of the posterior and different case-study experiments.
N. Lafon, R. Fablet, P. Naveau
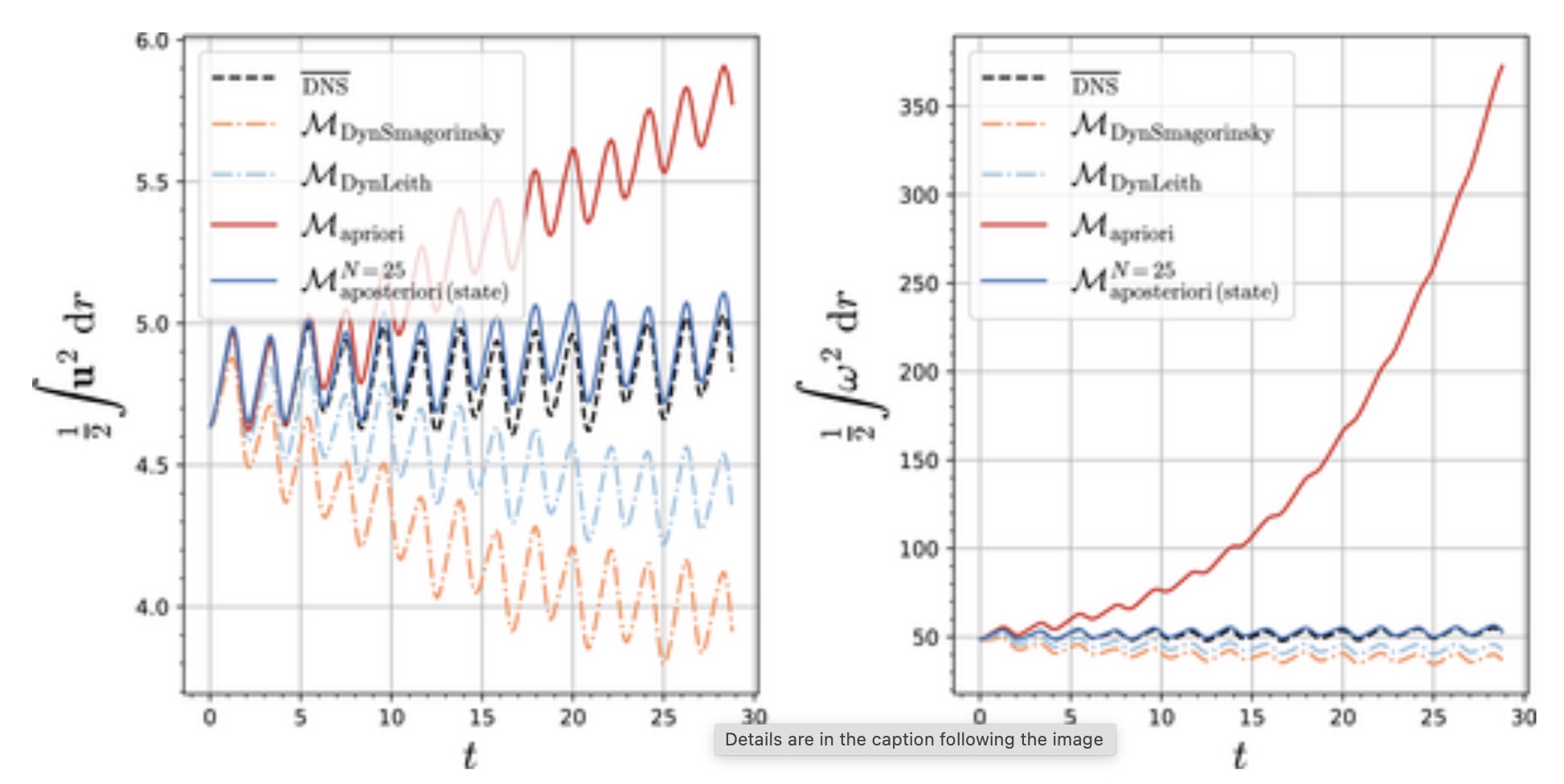
In this paper, we focus on the representation of energy backscatter in two-dimensional quasi-geostrophic turbulence and compare parametrizations obtained with different learning strategies at fixed computational complexity. We show that strategies based on a priori criteria yield parametrizations that tend to be unstable in direct simulations and describe how subgrid parametrizations can alternatively be trained end-to-end in order to meet a posteriori criteria. We illustrate that end-to-end learning strategies yield parametrizations that outperform known empirical and data-driven schemes in terms of performance, stability, and ability to apply to different flow configurations.
H. Frezat, J. Le Sommer, R. Fablet, G. Balarac, R. Lguensat.
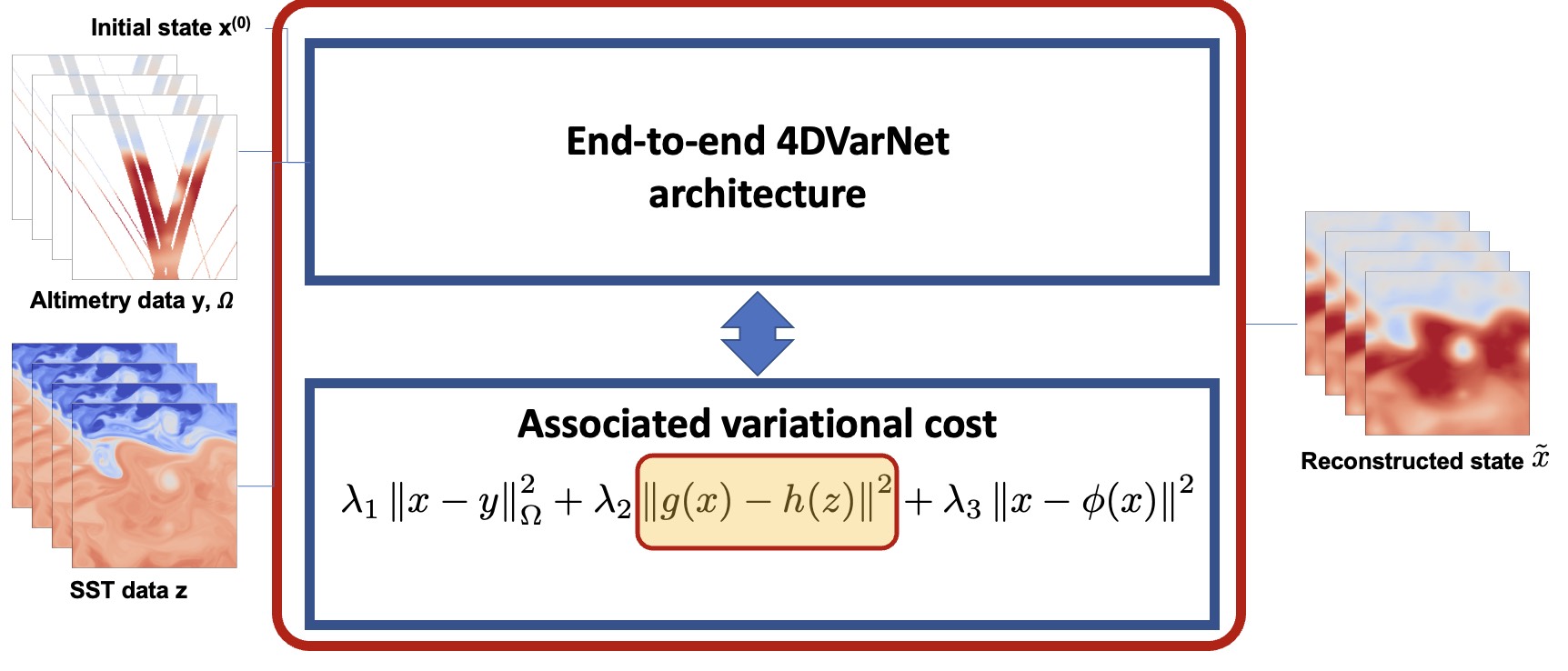
Due to the irregular space-time sampling of sea surface observations, the reconstruction of sea surface dynamics is a challenging inverse problem. While satellite altimetry provides a direct observation of the sea surface height (SSH), which relates to the divergence-free component of sea surface currents, the associated sampling pattern prevents from retrieving fine-scale sea surface dynamics, typically below a 10-day time scale. By contrast, other satellite sensors provide higher-resolution observations of sea surface tracers such as sea surface temperature (SST). Multimodal inversion schemes then arise as an appealing strategy. We introduce multimodal 4DVarNets and demonstrate their relevance for a Gulf Stream OSSE case-study.
R. Fablet, Q. Febvre, B. Chapron
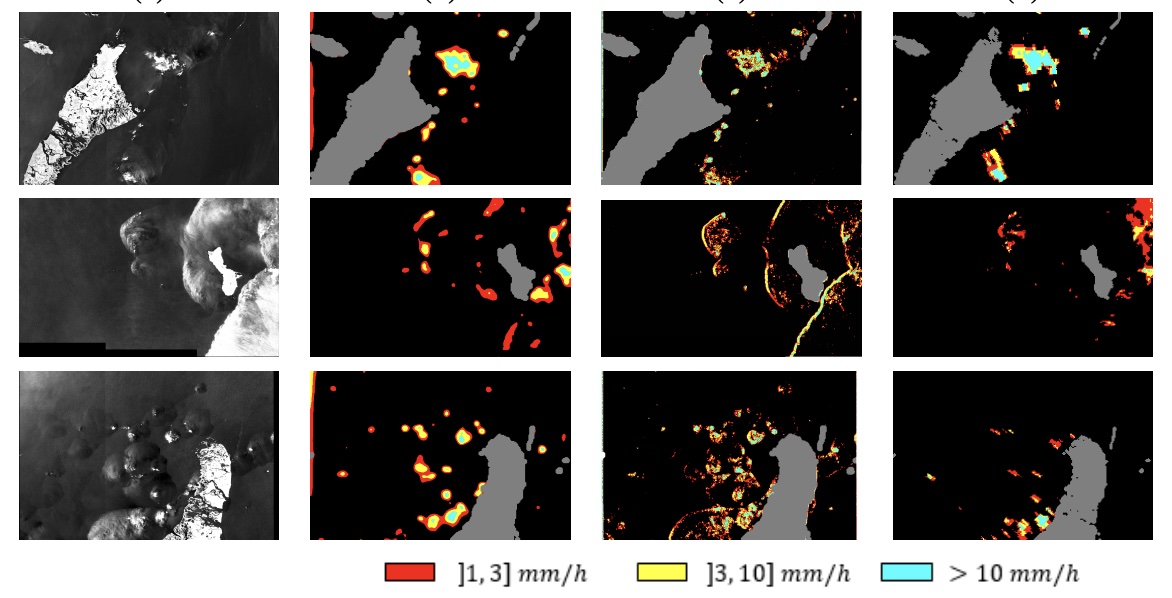
Remote sensing of rainfall events is critical for both operational and scientific needs. Ground-based weather radars, such as NOAA’s Next-Generation Radar (NEXRAD), provide reflectivity and precipitation measurements of rainfall events. However, the observation range of such radars is limited to a few hundred kilometers. Here we propose a deep learning approach to extract rainfall information from SAR imagery. We demonstrate that a convolutional neural network, such as U-Net, trained on a colocated and preprocessed Sentinel1-NEXRAD dataset clearly outperforms state-of-the-art filtering schemes.
A. Colin, P. Tandeo, C. Peureux, R. Husson, N. Longepe, Nicolas R. Fablet
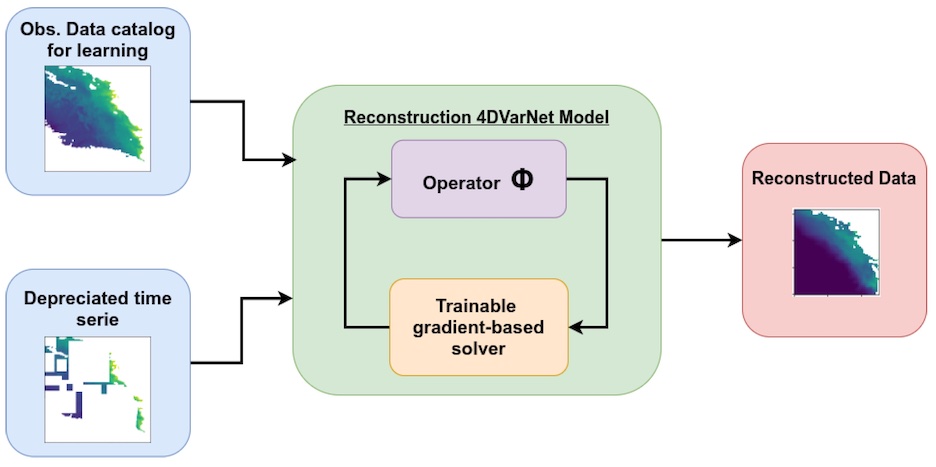
This paper addresses end-to-end neural interpolation of satellite-derived sea surface suspended sediment concentrations in coastal areas. It supports the applicability of 4DVarNet schemes to real satellite-derived datasets to outperform current interpolation schemes.
J.M. Vient, R. Fablet, F. Jourdin, C. Delacourt
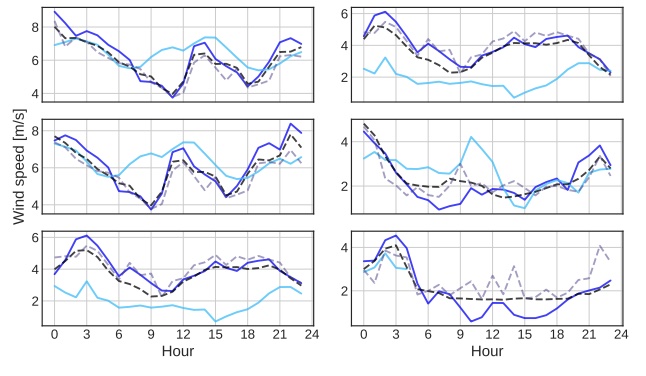
Wind speed retrieval at sea surface is of primary importance for scientific and operational applications. Here, we introduce a deep learning approach for the retrieval of wind speed time series from underwater acoustics possibly complemented by other data sources such as weather model reanalyses. Our approach bridges data assimilation and learning-based frameworks to benefit both from prior physical knowledge and computational efficiency. Numerical experiments on real data demonstrate that we outperform the state-of-the-art data-driven methods.
M. Zambra, D. Cazau, N. Farrugia, Alexandre Gensse, S. Pensieri, R. Bozzano, R. Fablet
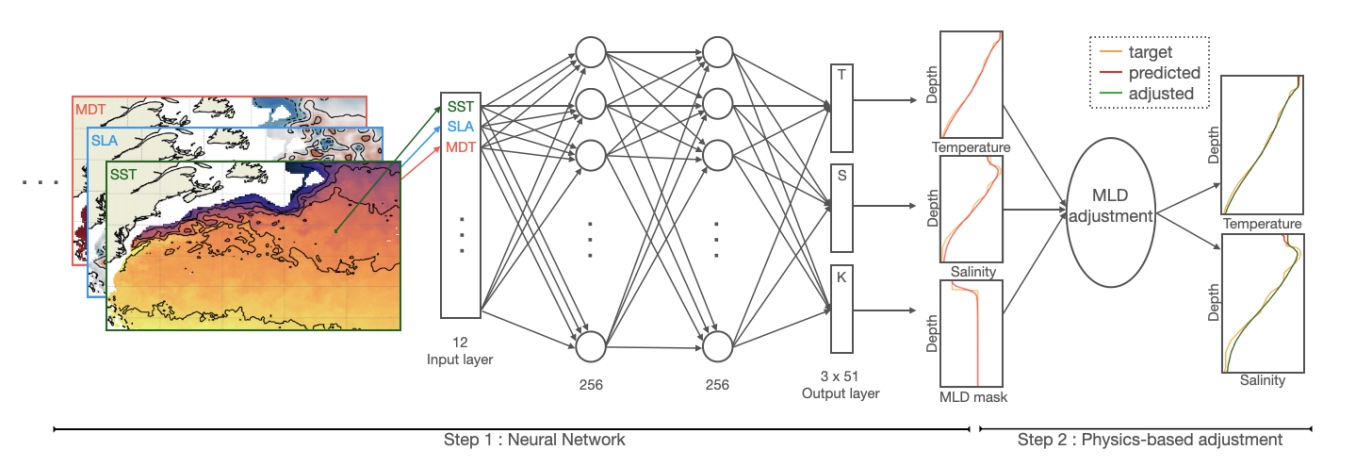
We introduce OSnet (Ocean Stratification network), a new ocean reconstruction system aimed at providing a physically consistent analysis of the upper ocean stratification. The proposed scheme is a bootstrapped 5 multilayer perceptron trained to predict simultaneously temperature and salinity profiles down to 1000m and the Mixed Layer Depth from surface data covering 1993 to 2019. OSnet is trained to fit sea surface temperature and sea level anomalies onto all historical in-situ profiles in the Gulf Stream region. We asses its relevance with respect to state-of-the-art products.
E. Pauthenet, L. Bachelot, K. Balem, G. Maze, A.-M. Treguier, F. Roquet, R. Fablet, P. Tandeo
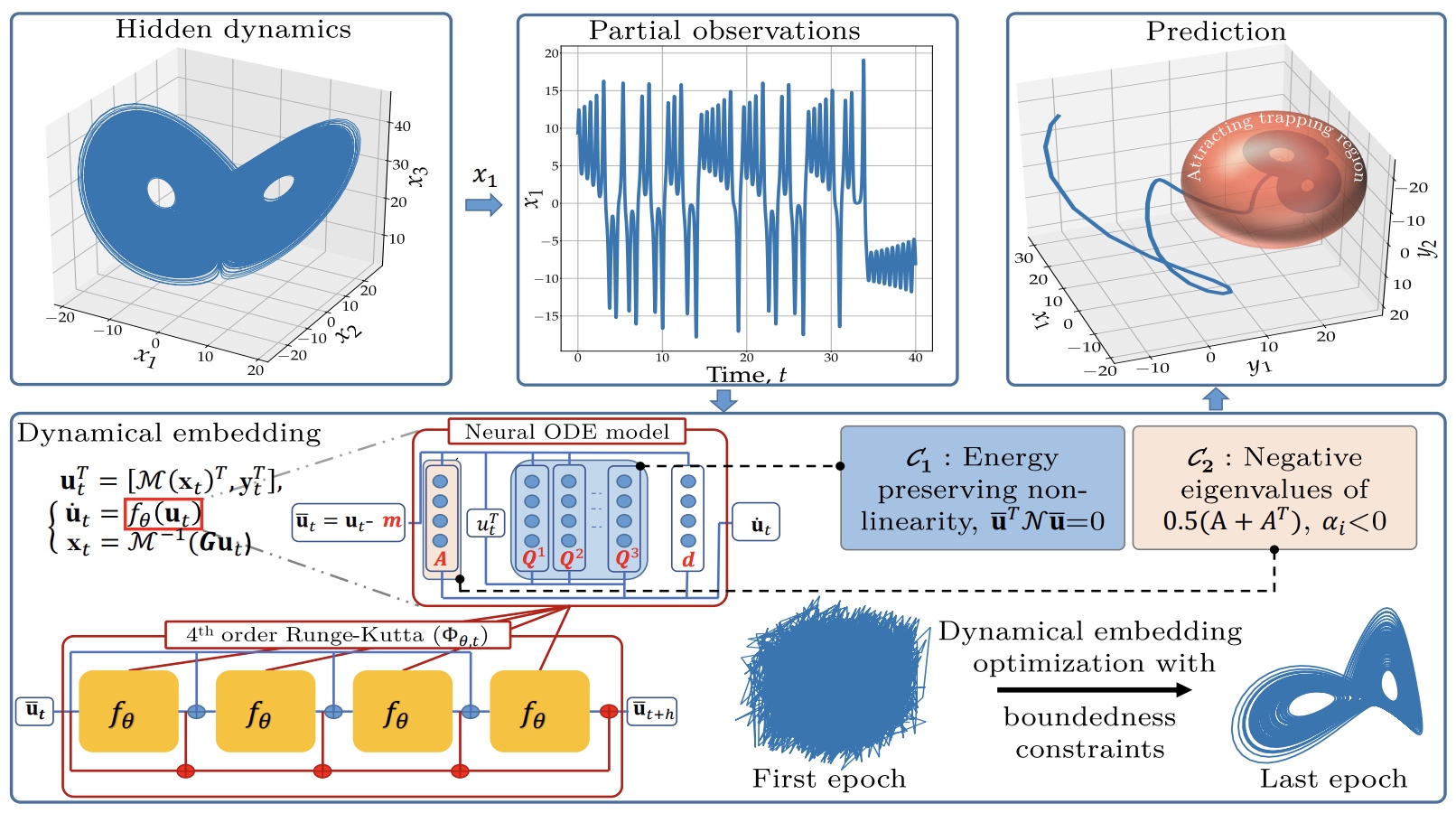
The identification of computationally-relevant representations of partially-observed and highly nonlinear systems is challenging and often limited to short-term forecast applications. Here, we investigate the physics-constrained learning of implicit dynamical embeddings, leveraging neural ordinary differential equation representations under boundedness constraint.
S. Ouala, S. Brunton, A. Pascual, B. Chapron, F. Collard, L. Gaultier, R. Fablet
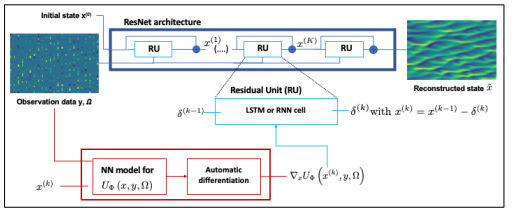
This paper introduces 4DVarNet, an end-to-end learning approach for variational data assimilation models and solvers. Reported results may question the design of operational data assimilation systems.
R Fablet, B. Chapron, L. Drumetz, E. Memin, O. Pannekoucke, F. Rousseau
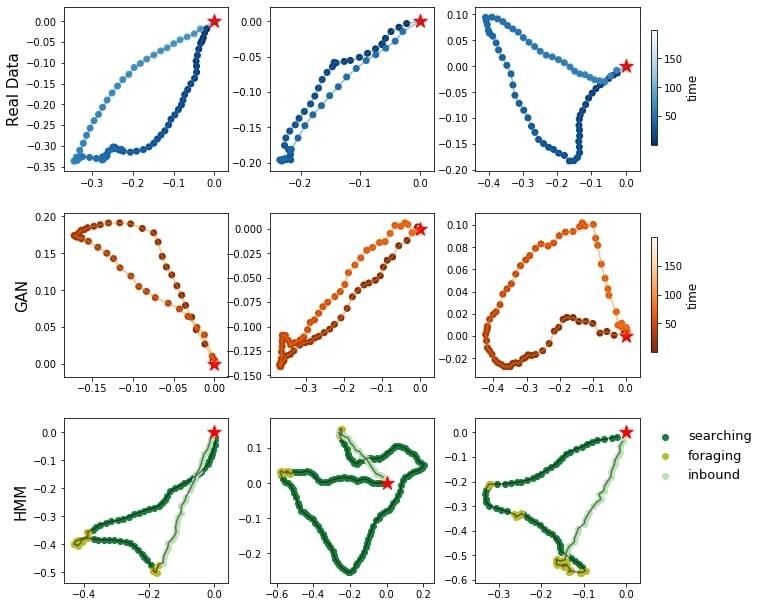
In this work, we investigate Generative Adversarial Networks (GAN) - for the simulation of animal trajectories. We demonstrate the outstanding ability of GANs to simulate ‘realistic’ seabirds foraging trajectories.
A. Roy, S. Lanco Bertrand, R. Fablet
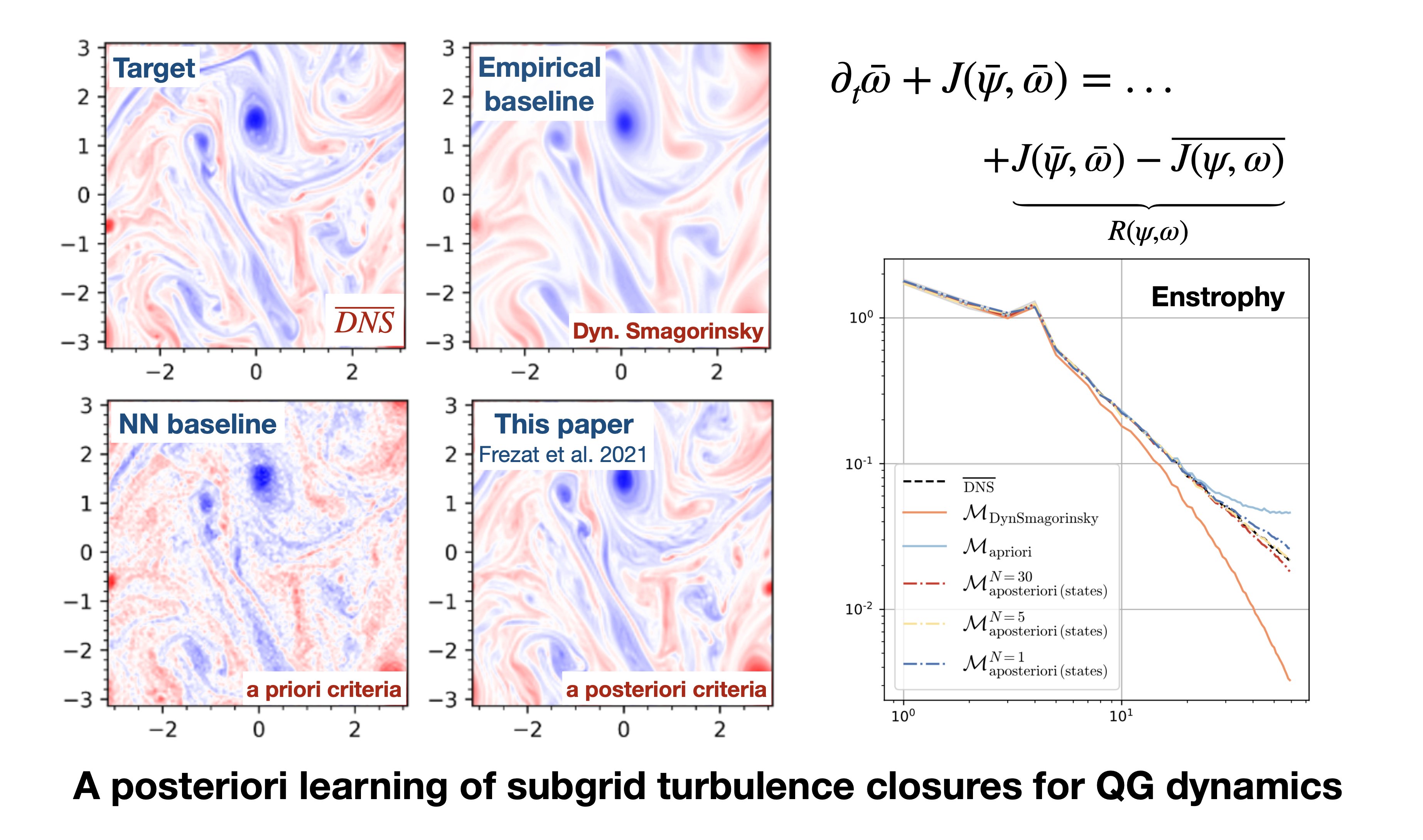
Modeling the subgrid-scale dynamics of reduced models is a long standing open problem that finds application in ocean, atmosphere and climate predictions where direct numerical simulation (DNS) is impossible. While neural networks (NNs) have already been applied to a range of three-dimensional flows with success, two dimensional flows are more challenging because of the backscatter of energy from small to large scales. We show that learning a model jointly with the dynamical solver and a meaningful a-posteriori-based loss function lead to stable and realistic simulations when applied to quasi-geostrophic turbulence.
Frezat, H., Sommer, J. L., Fablet, R., Balarac, G., Lguensat, R.
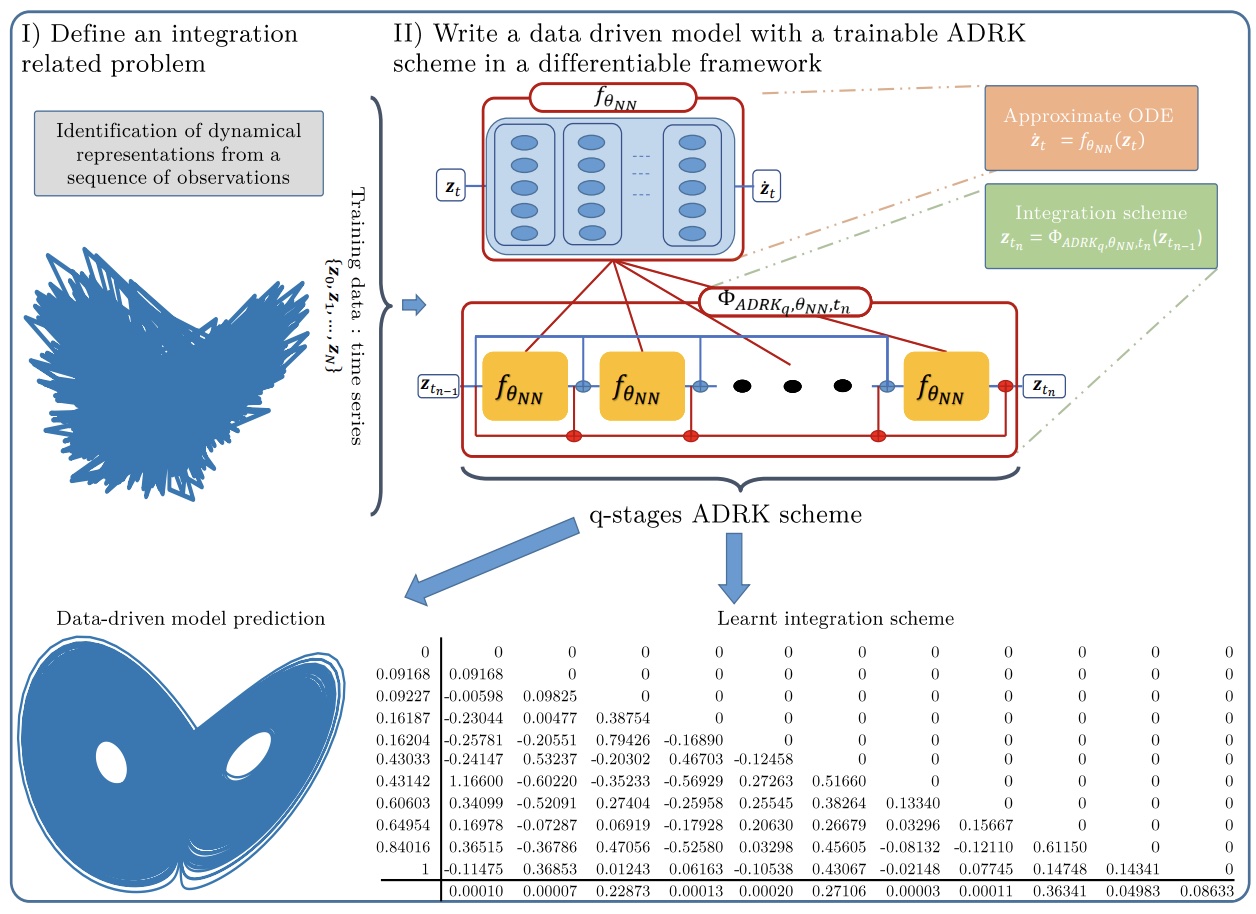
In this paper, we propose a novel framework to learn integration schemes that minimize an integration-related cost function. Especially, we demonstrate the relevance of the proposed learning-based approach for non-linear equations.
S. Ouala, L. Debreu, A. Pascual, B. Chapron, F. Collard, L. Gaultier, R. Fablet
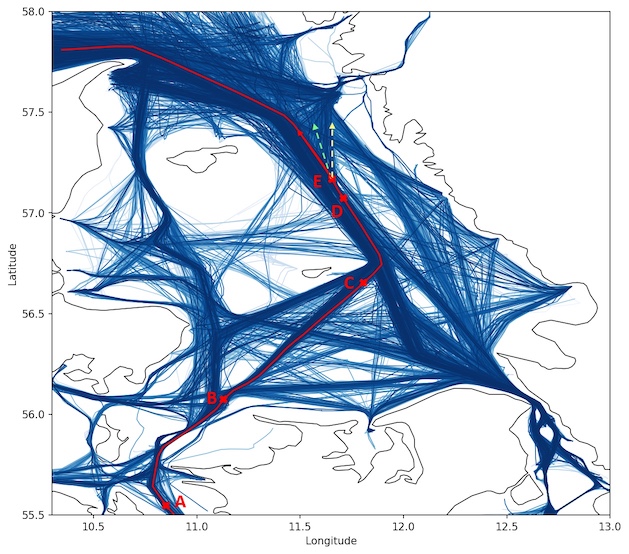
This paper presents TrAISformer-a generative transformer for AIS trajectory prediction. Compared with state-of-the-art approachs, it shows a great capacity to forecast maritime traffic trajectories few hours ahead in complex maritime traffic areas.
D. Nguyen, R Fablet

This paper introduces an end-to-end architecture for the joint interpolation and representation learning for irregularly-sampled observation data. As application case-studies, we consider ocean remote sensing datasets, which involve very large missing data rates.
R Fablet, L. Drumetz, M. Beauchamp, F. Rousseau
Front. in Applied Math and Statistics
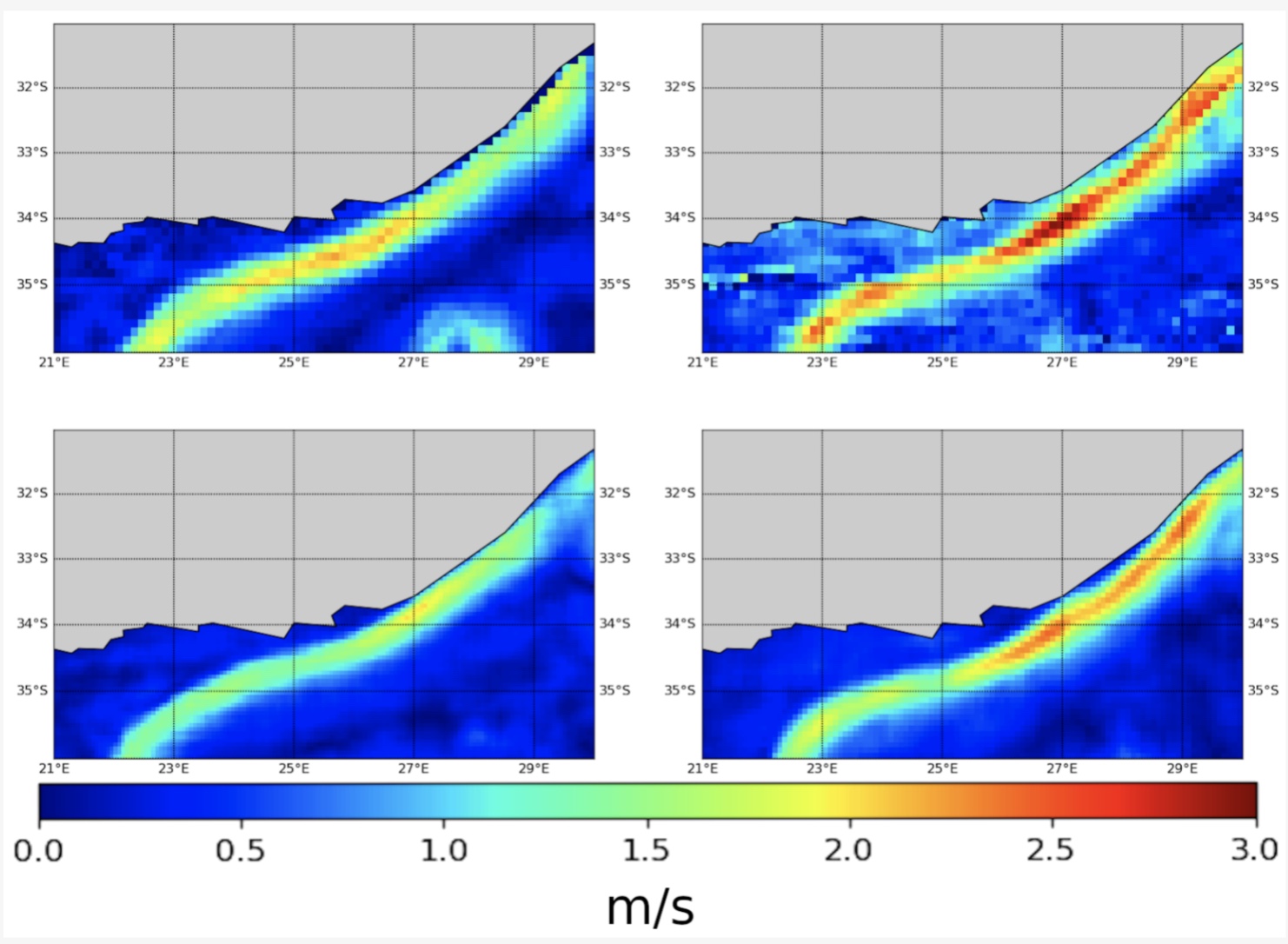
In this work we investigate the relevance of AIS data streams for the estimation of the surface current velocities. Using a physics-informed observation model, we propose to a trainable variational formulation. Numerical experiments on a real AIS dataset off South Africa support the relevance of the proposed approach to improve the reconstruction of sea surface current, including w.r.t. altimetry-based ones.
S. Benaïchouche, C. Legoff, Y. Guichoux, F. Rousseau, R. Fablet
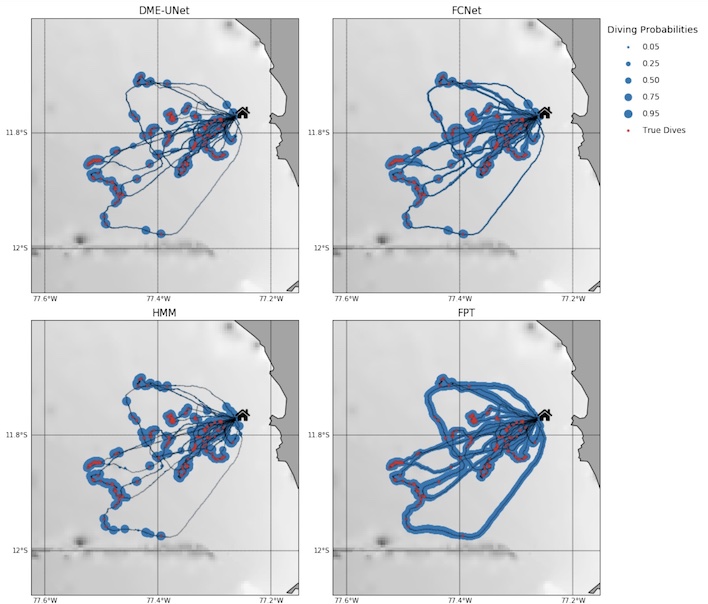
We propose a novel deep learning model for seabird trajectory data. Our CNN model considerably increases the ability of deep networks to infer seabird behaviours, as well as their stability to different data inputs.
A. Roy, S. Lanco-Bertrand, R Fablet
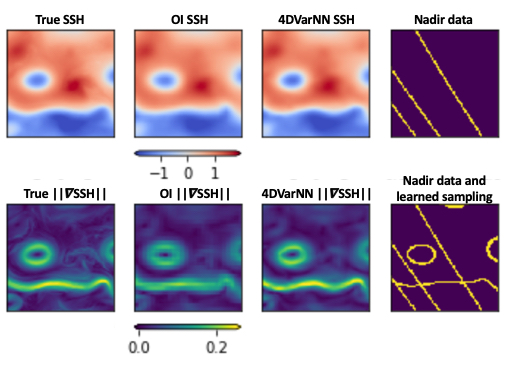
This paper presents different applications of 4DVarNN framework to satellite-derived sea surface dynamics, including learning-based optimal sampling strategies.
R Fablet, M.M. Amar, Q. Febvre, M. Beauchamp, B. Chapron

This paper introduces a novel data driven framework for the identification of ODE representations for partially observed systems.
S Ouala, D Nguyen, L Drumetz, B Chapron, A Pascual, F Collard, L Gaultier, R Fablet

Transformation invariances are shown to improve performance and generalization of NN models in the context of subgrid-scale turbulent modeling.
H Frezat, G Balarac, J Le Sommer, R Fablet, R Lguensat

Bridging state-of-the-art data assimilation and machine learning techniques to jointly reconstruct the true states and identify the governing equations of dynamical systems from series of noisy and partial data.
D Nguyen, S Ouala, L Drumetz, R Fablet
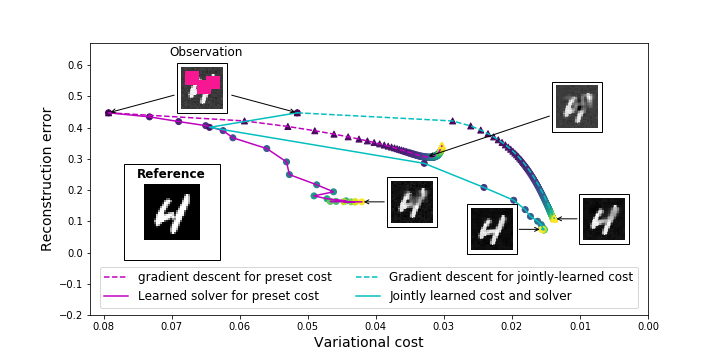
This paper introduces a novel data-driven framework to jointly learn variational models and the associated solvers to address inverse problems in signal and image processing, especially considering irregulary-sampled observation data.
R Fablet, L Drumetz, F Rousseau
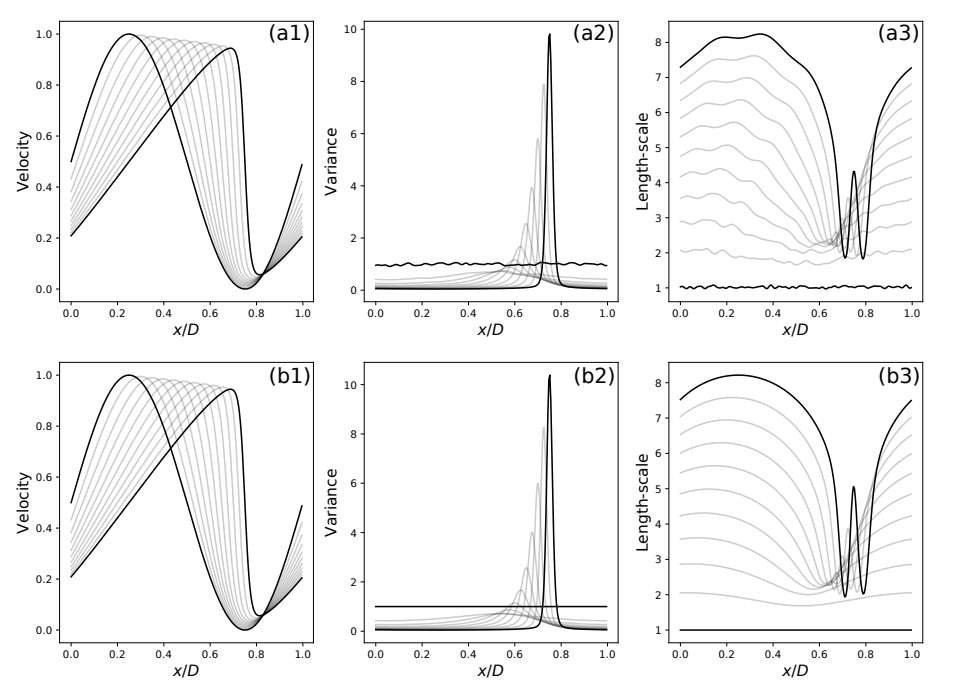
A first paper from the collaboration with O. Pannekoucke (Meteo France) addressing the automatic generation of neural network architectures from symbolic PDEs.
O Pannekoucke, R Fablet
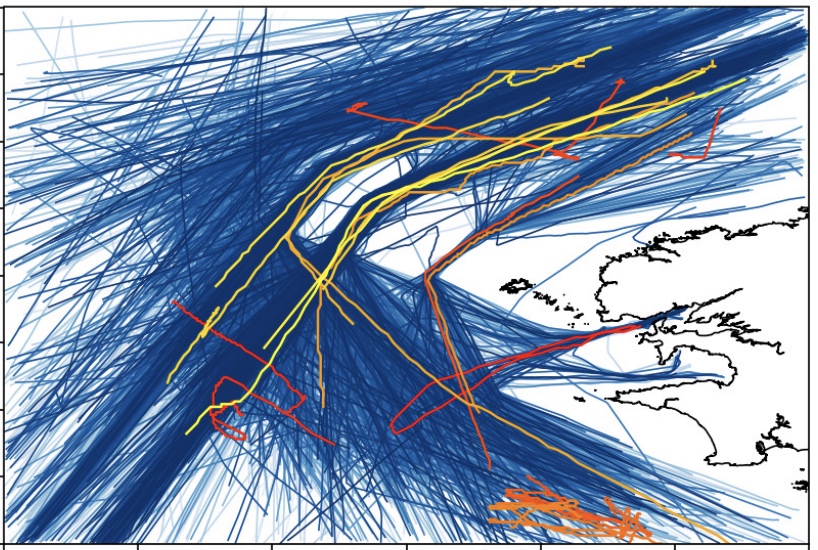
The presentation of GeoTrackNet framework for the detection of abnormal behaviours in AIS-based maritime traffic surveillance using variational deep learning.
D Nguyen, R Vadaine, G Hajduch, R Garello, R Fablet
IEEE TITS, 2020 (arXiv version)